Hoje vamos executar um modelo bem simples de aprendizado de máquina. Utilizaremos o Python através do Jupyter notebook e as bibliotecas scikit-learn, NumPy, Matplotlib e Pandas.
Nosso contexto é o seguinte: A Lanchonete Sanduixi (Fictícia) é especializada em fazer sanduíches a metro, ou como também é chamado em algumas regiões, sanduíche de metro. Em seu cardápio há uma série de tamanhos e seus respectivos preços, porém o nem todos os tamanhos estão presentes no menu. Por isso usaremos machine learning para termos uma previsão de preço de um sanduíche de 3 metros.
Em nosso caso da lanchonete, estamos assumindo que há uma relação direta entre o tamanho do sanduíche e seu preço final. E estamos desprezando qualquer outra variável que em um caso real, poderia interferir no preço, como sabor(ingredientes), localidade do estabelecimento, valor de entrega a domicílio e etc.
Para essa previsão usaremos o modelo de regressão linear simples. Esse modelo estuda a relação de uma variável dependente (preço) com uma variável independente (tamanho) através de dados históricos.
Muitas vezes no dia a dia, fazemos mentalmente algo similar a esse tipo de regressão. Por exemplo: Se sabemos que 8 pacotes de jujuba custam R$4 e que 2 pacotes custam R$1, logo, deduzimos que 4 pacotes devem custar R$2. E é bem isso que esse modelo de machine learning irá fazer, porém com valores não tão óbvios, já que a Sanduixi costuma dar um descontinho conforme maior for o sanduíche.
Bom, chega de papo e vamos aos códigos:
#Importar Matplotlib e Numpy import matplotlib.pyplot as plt import numpy as np %matplotlib inline
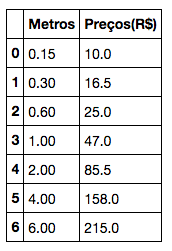
#Dados da Lanchonete fictícia Sanduixi #Metros(cm) Metros = [[0.15], [0.30], [0.60], [1], [2], [4], [6]] #Preços(R$) Precos = [[10], [16.50], [25], [47], [85.50], [158], [215]]
Note que há uma relação de progressão positiva de valores, mas não há uma constante. O preço do de 30cm é maior que o de 15cm, mas não é o dobro.
#Para visualizar melhor os dados:
from pandas import DataFrame
dados = {'Metros':[0.15, 0.30, 0.60, 1, 2, 4, 6],
'Preços(R$)':[10, 16.50, 25, 47, 85.50, 158, 215]}
frame = DataFrame(dados)
frame
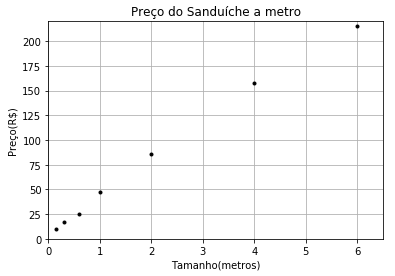
#Gráfico dos dados
plt.figure()
plt.xlabel('Tamanho(metros)')
plt.ylabel('Preço(R$)')
plt.title('Preço do Sanduíche a metro')
plt.plot(Metros, Precos, 'k.')
plt.axis([0, 6.5, 0, 220])
plt.grid(True)
plt.show()
#Gráfico para visualizar a correlação
fig, axs = plt.subplots(1, 2, figsize=(10, 5), sharey=True)
axs[0].plot(Metros, Precos, 'k.')
axs[1].plot(Metros, Precos, color = 'blue')
fig.suptitle('Pontos e Linha')
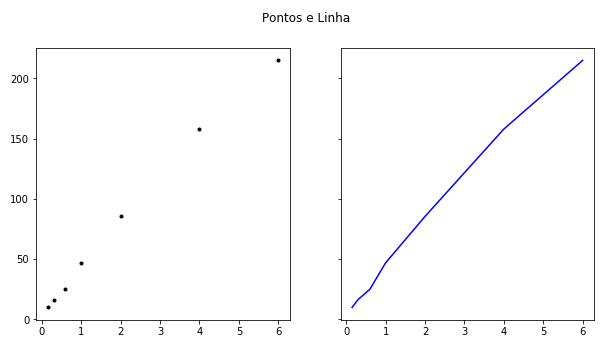
O diagrama de dispersão (pontos) e o de linha, sugerem que há uma correlação positiva entre as variáveis. Quanto maior o tamanho, maior o preço. Isso sugere que há uma relação linear entre eles. Gráficos que geram curvas revelam relações não lineares.
Alt+Tab:
Quando fazemos esse tipo análise é essencial que se verifique se realmente há uma ligação entre as duas variáveis para não se tirar conclusões e gerar informações erradas. Um exemplo hipotético: Um jornal publica um estudo que diz quanto mais carros com airbags andando pelas ruas, menores são os números de acidentes. Isso estaria correto?
Não, pois pode até existir uma relação numérica, mas o airbag em si, não evita acidentes, na verdade ele só é acionado quando há um acidente. O correto seria um estudo de como o uso de airbags reduz o número de mortes em acidentes. Ou o uso de freio ABS que diminui acidentes… Enfim, os dados podem ter uma relação proporcional positiva ou negativa, mas isso não significa que haja uma relação de causa-efeito. Por isso, faça uma análise detalhada, use raciocínio e bom senso.
Alt+Tab.
Continuando, vamos treinar o modelo com os dados que temos. Como são poucos, usaremos poucos. Quando temos mais dados, geralmente separamos em três partes: treino, teste e validação.
#Importar módulo de Regressão Linear do scikit-learn from sklearn.linear_model import LinearRegression #Preparando os dados de treino #Dados dos metros. X = [[0.15], [0.30], [0.60], [1], [2], [4], [6]] #Dados dos preços. Y = [[10], [16.50], [25], [47], [85.50], [158], [215]] #Treinar o modelo modelo.fit(X, Y)
A regressão linear funciona com a seguinte fórmula matemática:
Y = αX + β
O modelo usa os valores de Y e X que fornecemos para treino para descobrir os coeficientes α e β. Com o treino concluído e o modelo ciente dos coeficientes, vamos fornecer um valor de X para que ele possa prever o Y correspondente:
#Prever o preço de um sanduíche de 3 metros
print("Um sanduíche de 3 metros deve custar: R$%.2f" % modelo.predict([3][0]))

Usamos o Score para vermos o quão preciso está nosso algoritmo:
#Score de variação: 1 representa predição perfeita
print('Score de variação: %.2f' % modelo.score(X, Y))
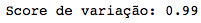
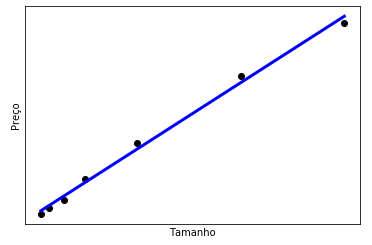
Podemos também montar um gráfico com a nossa linha de previsões:
#Gráfico representando a regressão linear (linha azul)
plt.scatter(X, Y, color = 'black')
plt.plot(X, modelo.predict(X), color = 'blue', linewidth = 3)
plt.xlabel('Tamanho')
plt.ylabel('Preço')
plt.xticks(())
plt.yticks(())
plt.show()
11-08-2018 | Update:
Pra quem quiser, segue o link do Github com o código.